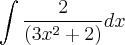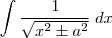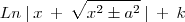Ola pessoal. Gostaria muito da ajuda de vocês pra entender Centro da massa. Eu tenho essas duas questões, alguem poderia me ajudar? 1)Use integrais para achar o centro de massa de um triangulo (0,0) (2,0)(0,8). 2)Use integrais para achar o centro de massa de um retângulo (1,-3)(4,-3)(4,5)(1,5) ...