Pesquisa resultou em 1 ocorrência
Voltar à pesquisa avançada
Encontrei dificuldades de iniciar e consequentemente solucionar ( encontrar o limite ) dessa função :
Calcular o limite de

quando
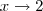
de:
![f(x)=\frac {\sqrt[3]{x} - \sqrt[3]{2}}{x - 2} f(x)=\frac {\sqrt[3]{x} - \sqrt[3]{2}}{x - 2}](/latexrender/pictures/bdc4d36061c092e195be030223e6301f.png)
Resposta :
![\frac {1}{3} \sqrt[3]{4} \frac {1}{3} \sqrt[3]{4}](/latexrender/pictures/5f4820dfbea938804656bdc7fb1274b7.png)
ou
![\frac {\sqrt[3]4} {3} \frac {\sqrt[3]4} {3}](/latexrender/pictures/1754945835f904a8968b08a1b1e2cbf2.png)
- por lo4dd
- Ter Mai 22, 2012 12:08
-
- Fórum: Cálculo: Limites, Derivadas e Integrais
- Tópico: Limites
- Respostas: 1
- Exibições: 847
Voltar à pesquisa avançada
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 quando
quando 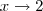 de:
de:![f(x)=\frac {\sqrt[3]{x} - \sqrt[3]{2}}{x - 2} f(x)=\frac {\sqrt[3]{x} - \sqrt[3]{2}}{x - 2}](/latexrender/pictures/bdc4d36061c092e195be030223e6301f.png)
![\frac {1}{3} \sqrt[3]{4} \frac {1}{3} \sqrt[3]{4}](/latexrender/pictures/5f4820dfbea938804656bdc7fb1274b7.png) ou
ou ![\frac {\sqrt[3]4} {3} \frac {\sqrt[3]4} {3}](/latexrender/pictures/1754945835f904a8968b08a1b1e2cbf2.png)