

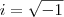 é uma definição, isto é, um atributo que foi convencionado e que, a rigor, não pode ser demonstrado.
é uma definição, isto é, um atributo que foi convencionado e que, a rigor, não pode ser demonstrado.ckde escreveu:Desculpem, realmente ficou difícil sem usar o LaTeX... A questão tem um errinho. O certo é: sejaum número primo que divide o número
, é ab + cd e não abcd

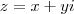 , se
, se 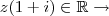
![Im[(x+yi)(1+i)]=0 Im[(x+yi)(1+i)]=0](/latexrender/pictures/267cf0a95cba192e172f41917b1d433c.png)
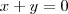 que corresponde a equação da bissetriz dos quadrantes pares. Portanto Letra E
que corresponde a equação da bissetriz dos quadrantes pares. Portanto Letra E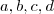 , existe um primo
, existe um primo  , diferente dos supracitados, que divide o número
, diferente dos supracitados, que divide o número 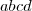
Anderson POntes escreveu:TOM ESTAVA PENSANDO EM RESOLVER COM PA , MAS NAO SEI COMO RESOLVER, SERÁ QUE É EM PA MESMO?
PeIdInHu escreveu:faltou a raiz cubica...?
![\sqrt[3]{3} \sqrt[3]{3}](/latexrender/pictures/00183145853114fdd8d947a663084fb6.png)