


 . Não é necessário calcular esta integral, no entanto, pois a área é simétrica, logo basta calcular a primeira e multiplicar por dois.
. Não é necessário calcular esta integral, no entanto, pois a área é simétrica, logo basta calcular a primeira e multiplicar por dois. for invertível, mas diferentes caso contrário.
for invertível, mas diferentes caso contrário. , logo
, logo  .
. é que quando falamos de formas diferenciais, existe o Lema de Poincaré que diz que
é que quando falamos de formas diferenciais, existe o Lema de Poincaré que diz que  , ou seja, o operador diferencial é nilpotente.
, ou seja, o operador diferencial é nilpotente. .
. . O que acontece é que
. O que acontece é que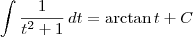 ,
,