


 .
. , então a equação do enunciado não terá grau dois! Com efeito, perderá sentido o termo "raízes sempre distintas".
, então a equação do enunciado não terá grau dois! Com efeito, perderá sentido o termo "raízes sempre distintas".Ewerton Alves escreveu:Isole "A" na Fórmula
St = 0,9 ⋅ (0,7 ⋅ (S3+S4) + (A))
![\\ St = 0,9 \cdot \left [ 0,7 \cdot (S3 + S4) + A \right ] \\\\ \frac{St}{0,9} = 0,7 \cdot (S3 + S4) + A \\\\ \boxed{A = \frac{St}{0,9} - 0,7 (S3 + S4)} \\ St = 0,9 \cdot \left [ 0,7 \cdot (S3 + S4) + A \right ] \\\\ \frac{St}{0,9} = 0,7 \cdot (S3 + S4) + A \\\\ \boxed{A = \frac{St}{0,9} - 0,7 (S3 + S4)}](/latexrender/pictures/eb21af7a60925f3fad5f98d5ea8c21e6.png)
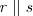 e
e 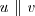 , possivelmente, poderá obter a resposta utilizando os conceitos envolvendo Semelhança de triângulos.
, possivelmente, poderá obter a resposta utilizando os conceitos envolvendo Semelhança de triângulos.